4 Argument

At school, at work, and in everyday life, argument is one of main ways we exchange ideas with one another.  Academics, business people, scientists, and other professionals all make arguments to determine what to do or think, or to solve a problem by enlisting others to do or believe something they otherwise would not.  Not surprisingly, then, argument dominates writing, and training in argument writing is essential for all college students.

This chapter will explore how to define argument and how to talk about arguments.

 

1.       What Is Argument?

2.       What Are the Components and Vocabulary of Argument?

1.  What Is Argument?

All people, including you, make arguments on a regular basis.  When you make a claim and then support the claim with reasons, you are making an argument. Consider the following:

• If, as a teenager, you ever made a case for borrowing your parents’ car using reasonable support—a track record of responsibility in other areas of your life, a good rating from your driving instructor, and promises to follow rules of driving conduct laid out by your parents—you have made an argument.

 

• If, as an employee, you ever persuaded your boss to give you a raise using concrete evidence—records of sales increases in your sector, a work calendar with no missed days, and personal testimonials from satisfied customers—you have made an argument.

 

• If, as a gardener, you ever shared your crops at a farmer’s market, declaring that your produce is better than others using relevant support—because you used the most appropriate soil, water level, and growing time for each crop—you’ve made an argument.

 

• If, as a literature student, you ever wrote an essay on your interpretation of a poem—defending your ideas with examples from the text and logical explanations for how those examples demonstrate your interpretation—you have made an argument.

 

The two main models of argument desired in college courses as part of the training for academic or professional life are rhetorical argument and academic argument.  If rhetoric is the study of the craft of writing and speaking, particularly writing or speaking designed to convince and persuade, the student studying rhetorical argument focuses on how to create an argument that convinces and persuades effectively.  To that end, the student must understand how to think broadly about argument, the particular vocabulary of argument, and the logic of argument.  The close sibling of rhetorical argument is academic argument, argument used to discuss and evaluate ideas, usually within a professional field of study, and to convince others of those ideas. In academic argument, interpretation and research play the central roles.

However, it would be incorrect to say that academic argument and rhetorical argument do not overlap.  Indeed, they do, and often.  A psychologist not only wishes to prove an important idea with research, but she will also wish to do so in the most effective way possible.  A politician will want to make the most persuasive case for his side, but he should also be mindful of data that may support his points.  Thus, throughout this chapter, when you see the term argument, it refers to a broad category including both rhetorical and academic argument.

Before moving to the specific parts and vocabulary of argument, it will be helpful to consider some further ideas about what argument is and what it is not.

Argument vs. Controversy or Fight

Consumers of written texts are often tempted to divide writing into two categories: argumentative and non-argumentative. According to this view, to be argumentative, writing must have the following qualities: It has to defend a position in a debate between two or more opposing sides, it must be on a controversial topic, and the goal of such writing must be to prove the correctness of one point of view over another.

A related definition of argument implies a confrontation, a clash of opinions and personalities, or just a plain verbal fight. It implies a winner and a loser, a right side and a wrong one. Because of this understanding of the word “argument,” many students think the only type of argument writing is the debate-like position paper, in which the author defends his or her point of view against other, usually opposing, points of view.

These two characteristics of argument—as controversial and as a fight—limit the definition because arguments come in different disguises, from hidden to subtle to commanding. It is useful to look at the term “argument” in a new way. What if we think of argument as an opportunity for conversation, for sharing with others our point of view on an issue, for showing others our perspective of the world? What if we think of argument as an opportunity to connect with the points of view of others rather than defeating those points of view?

One community that values argument as a type of communication and exchange is the community of scholars.  They advance their arguments to share research and new ways of thinking about topics.  Biologists, for example, do not gather data and write up analyses of the results because they wish to fight with other biologists, even if they disagree with the ideas of other biologists.  They wish to share their discoveries and get feedback on their ideas.  When historians put forth an argument, they do so often while building on the arguments of other historians who came before them.  Literature scholars publish their interpretations of different works of literature to enhance understanding and share new views, not necessarily to have one interpretation replace all others.  There may be debates within any field of study, but those debates can be healthy and constructive if they mean even more scholars come together to explore the ideas involved in those debates.  Thus, be prepared for your college professors to have a much broader view of argument than a mere fight over a controversial topic or two.

Argument vs. Opinion

Argument is often confused with opinion.  Indeed, arguments and opinions sound alike.  Someone with an opinion asserts a claim that he thinks is true.  Someone with an argument asserts a claim that she thinks is true.  Although arguments and opinions do sound the same, there are two important differences:

1. Arguments have rules; opinions do not.  In other words, to form an argument, you must consider whether the argument is reasonable.  Is it worth making?  Is it valid?  Is it sound?  Do all of its parts fit together logically?  Opinions, on the other hand, have no rules, and anyone asserting an opinion need not think it through for it to count as one; however, it will not count as an argument.
2. Arguments have support; opinions do not.  If you make a claim and then stop, as if the claim itself were enough to demonstrate its truthfulness, you have asserted an opinion only.  An argument must be supported, and the support of an argument has its own rules.  The support must also be reasonable, relevant, and sufficient.

 

Figure 3.1 “Opinion vs Argument”

 

Argument vs. Thesis

Another point of confusion is the difference between an argument and an essay’s thesis.  For college essays, there is no essential difference between an argument and a thesis; most professors use these terms interchangeably.  An argument is a claim that you must then support.  The main claim of an essay is the point of the essay and provides the purpose for the essay.  Thus, the main claim of an essay is also the thesis. For more on the thesis, see Chapter 4, “The Writing Process.”

Consider this as well: Most formal essays center upon one main claim (the thesis) but then support that main claim with supporting evidence and arguments.  The topic sentence of a body paragraph can be another type of argument, though a supporting one, and, hence, a narrower one.  Try not to be confused when professors call both the thesis and topic sentences arguments.  They are not wrong because arguments come in different forms; some claims are broad enough to be broken down into a number of supporting arguments.  Many longer essays are structured by the smaller arguments that are a part of and support the main argument.  Sometimes professors, when they say supporting points or supporting arguments, mean the reasons (premises) for the main claim (conclusion) you make in an essay.  If a claim has a number of reasons, those reasons will form the support structure for the essay, and each reason will be the basis for the topic sentence of its body paragraph.

 

Argument vs. Fact

Arguments are also commonly mistaken for statements of fact.  This comes about because often people privilege facts over opinions, even as they defend the right to have opinions.  In other words, facts are “good,” and opinions are “bad,” or if not exactly bad, then fuzzy and thus easy to reject.  However, remember the important distinction between an argument and an opinion stated above: While argument may sound like an opinion, the two are not the same.  An opinion is an assertion, but it is left to stand alone with little to no reasoning or support. An argument is much stronger because it includes and demonstrates reasons and support for its claim.

As for mistaking a fact for an argument, keep this important distinction in mind: An argument must be arguable.  In everyday life, arguable is often a synonym for doubtful.  For an argument, though, arguable means that it is worth arguing, that it has a range of possible answers, angles, or perspectives: It is an answer, angle, or perspective with which a reasonable person might disagree.  Facts, by virtue of being facts, are not arguable.  Facts are statements that can be definitely proven using objective data. The statement that is a fact is absolutely valid. In other words, the statement can be pronounced as definitively true or definitively false. For example, 2 + 2 = 4. This expression identifies a verifiably true statement, or a fact, because it can be proved with objective data.  When a fact is established, there is no other side, and there should be no disagreement.

The misunderstanding about facts (being inherently good) and argument (being inherently problematic because it is not a fact) leads to the mistaken belief that facts have no place in an argument.  This could not be farther from the truth.  First of all, most arguments are formed by analyzing facts.  Second, facts provide one type of support for an argument.  Thus, do not think of facts and arguments as enemies; rather, they work closely together.

 

Explicit vs. Implicit Arguments

Arguments can be both explicit and implicit. Explicit arguments contain prominent and definable thesis statements and multiple specific proofs to support them. This is common in academic writing from scholars of all fields.  Implicit arguments, on the other hand, work by weaving together facts and narratives, logic and emotion, personal experiences and statistics. Unlike explicit arguments, implicit ones do not have a one-sentence thesis statement. Implicit arguments involve evidence of many different kinds to build and convey their point of view to their audience. Both types use rhetoric, logic, and support to create effective arguments.

 

Argument and Rhetoric

An argument in written form involves making choices, and knowing the principles of rhetoric allows a writer to make informed choices about various aspects of the writing process. Every act of writing takes place in a specific rhetorical situation. The most basic and important components of a rhetorical situation are

• Author of the text.
• Purpose of the text.
• Intended audience (i.e., those the author imagines will be reading the text).
• Form or type of text.

These components give readers a way to analyze a text on first encounter.  These factors also help writers select their topics, arrange their material, and make other important decisions about the argument they will make and the support they will need.  For more on rhetoric, see Chapter 2, “Rhetorical Analysis.”

 

2. What Are the Components and Vocabulary of Argument?

Questions are at the core of arguments. What matters is not just that you believe that what you have to say is true, but that you give others viable reasons to believe it as well—and also show them that you have considered the issue from multiple angles. To do that, build your argument out of the answers to the five questions a rational reader will expect answers to.  In academic and professional writing, we tend to build arguments from the answers to these main questions:

1. What do you want me to do or think?
2. Why should I do or think that?
3. How do I know that what you say is true?
4. Why should I accept the reasons that support your claim?
5. What about this other idea, fact, or consideration?
6. How should you present your argument?

When you ask people to do or think something they otherwise would not, they quite naturally want to know why they should do so. In fact, people tend to ask the same questions. As you make a reasonable argument, you anticipate and respond to readers’ questions with a particular part of argument:

1. The answer to What do you want me to do or think? is your conclusion: “I conclude that you should do or think X.”

2. The answer to Why should I do or think that? states your premise: “You should do or think X because . . .”

3. The answer to How do I know that what you say is true? presents your support: “You can believe my reasons because they are supported by these facts . . .”

4. The answer to Why should I accept that your reasons support your claim? states your general principle of reasoning, called a warrant: “My specific reason supports my specific claim because whenever this general condition is true, we can generally draw a conclusion like mine.”

5. The answer to What about this other idea, fact, or conclusion?acknowledges that your readers might see things differently and then responds to their counterarguments.

6. The answer to How should you present your argument? leads to the point of view, organization, and tone that you should use when making your arguments.

As you have noticed, the answers to these questions involve knowing the particular vocabulary about argument because these terms refer to specific parts of an argument.  The remainder of this section will cover the terms referred to in the questions listed above as well as others that will help you better understand the building blocks of argument.

What Is a Conclusion, and What Is a Premise?

The root notion of an argument is that it convinces us that something is true. What we are being convinced of is the conclusion. An example would be this claim:

Littering is harmful.

A reason for this conclusion is called the premise. Typically, a conclusion will be supported by two or more premises. Both premises and conclusions are statements.  Some premises for our littering conclusion might be these:

       Littering is dangerous to animals.

       Littering is dangerous to humans.

Thus, to be clear, understand that an argument asserts that the writer’s claim is true in two main parts: the premises of the argument exist to show that the conclusion is true.

 

What Is a Statement?

A statement is a type of sentence that can be true or false and corresponds to the grammatical category of a declarative sentence. For example, the sentence,

The Nile is a river in northeastern Africa,

is a statement because it makes sense to inquire whether it is true or false. (In this case, it happens to be true.) However, a sentence is still a statement, even if it is false. For example, the sentence,

The Yangtze is a river in Japan,

is still a statement; it is just a false statement (the Yangtze River is in China). In contrast, none of the following sentences are statements:

Please help yourself to more casserole.

Don’t tell your mother about the surprise.

Do you like Vietnamese pho?

None of these sentences are statements because it does not make sense to ask whether those sentences are true or false; rather, they are a request, a command, and a question, respectively.  Make sure to remember the difference between sentences that are declarative statements and sentences that are not because arguments depend on declarative statements.

 

To reiterate: All arguments are composed of premises and conclusions, both of which are types of statements. The premises of the argument provide reasons for thinking that the conclusion is true. Arguments typically involve more than one premise.

What Is Standard Argument Form?

A standard way of capturing the structure of an argument, or diagramming it, is by numbering the premises and conclusion.  For example, the following represents another way to arrange the littering argument:

1. Littering is harmful
2. Litter is dangerous to animals
3. Litter is dangerous to humans

This numbered list represents an argument that has been put into standard argument form.  A more precise definition of an argument now emerges, employing the vocabulary that is specific to academic and rhetorical arguments. An argument is a set of statements, some of which (the premises: statements 2 and 3 above) attempt to provide a reason for thinking that some other statement (the conclusion: statement 1) is true.

 

Figure 3.2 “Argument Diagram”

Recognizing arguments is essential to analysis and critical thinking; if you cannot distinguish between the details (the support) of a piece of writing and what those details are there to support (the argument), you will likely misunderstand what you are reading.  Additionally, studying how others make arguments can help you learn how to effectively create your own.

What Are Argument Indicators?

While mapping an argument in standard argument form can be a good way to figure out and formulate a thesis, identifying arguments by other writers is also important.  The best way to identify an argument is to ask whether a claim exists (in statement form) that a writer justifies by reasons (also in statement form). Other identifying markers of arguments are key words or phrases that are premise indicators or conclusion indicators. For example, recall the littering argument, reworded here into a single sentence (much like a thesis statement):

Littering is harmful because it is dangerous to both animals and humans.

The word “because” here is a premise indicator. That is, “because” indicates that what follows is a reason for thinking that littering is bad. Here is another example:

The student plagiarized since I found the exact same sentences on a website, and the website was published more than a year before the student wrote the paper.

In this example, the word “since” is a premise indicator because what follows is a statement that is clearly intended to be a reason for thinking that the student plagiarized (i.e., a premise). Notice that in these two cases, the premise indicators “because” and “since” are interchangeable: “because” could be used in place of “since” or “since” in the place of “because,” and the meaning of the sentences would have been the same.

Figure 3.3 “Common Premise Indicators”

In addition to premise indicators, there are also conclusion indicators. Conclusion indicators mark that what follows is the conclusion of an argument. For example,

Bob-the-arsonist has been dead for a year, so Bob-the-arsonist didn’t set the fire at the East Lansing Starbucks last week.

In this example, the word “so” is a conclusion indicator because what follows it is a statement that someone is trying to establish as true (i.e., a conclusion). Here is another example of a conclusion indicator:

A poll administered by Gallup (a respected polling company) showed candidate X to be substantially behind candidate Y with only a week left before the vote; therefore, candidate Y will probably not win the election.

In this example, the word “therefore” is a conclusion indicator because what follows it is a statement that someone is trying to establish as true (i.e., a conclusion). As before, in both of these cases, the conclusion indicators “so” and “therefore” are interchangeable: “So” could be used in place of “therefore” or “therefore” in the place of “so,” and the meaning of the sentences would have been the same.

Figure 3.4 “Common Conclusion Indicators”

 

What Constitutes Support?

To ensure that your argument is sound—that the premises for your conclusion are true—you must establish support.  The burden of proof, to borrow language from law, is on the one making an argument, not on the recipient of an argument.  If you wish to assert a claim, you must then also support it, and this support must be relevant, logical, and sufficient.

It is important to use the right kind of evidence, to use it effectively, and to have an appropriate amount of it.

• If, for example, your philosophy professor did not like that you used a survey of public opinion as your primary evidence in an ethics paper, you most likely used material that was not relevant to your topic.  Rather, you should find out what philosophers count as good evidence. Different fields of study involve types of evidence based on relevance to those fields.

 

• If your professor has put question marks by your thesis or has written, “It does not follow,” you likely have problems with logic.  Make sure it is clear how the parts of your argument logically fit together.

 

• If your instructor has told you that you need more analysis, suggested that you are “just listing” points or giving a “laundry list,” you likely have not included enough explanation for how a point connects to and supports your argument, which is another problem with logic, this time related to the warrants of your argument. You need to fully incorporate evidence into your argument. (See more on warrants immediately below.)

 

• If you see comments like “for example?,” “proof?,” “go deeper,” or “expand,” you may need more evidence.  In other words, the evidence you have is not yet sufficient.  One or two pieces of evidence will not be enough to prove your argument.  Similarly, multiple pieces of evidence that aren’t developed thoroughly would also be flawed, also insufficient. Would a lawyer go to trial with only one piece of evidence?  No, the lawyer would want to have as much evidence as possible from a variety of sources to make a viable case.  Similarly, a lawyer would fully develop evidence for a claim using explanation, facts, statistics, stories, experiences, research, details, and the like.

You will find more information about the different types of evidence, how to find them, and what makes them credible in Chapter 6, “Research.”  Logic will be covered later on in this chapter.

What Is the Warrant?

Above all, connect the evidence to the argument.  This connection is the warrant.  Evidence is not self-evident.  In other words, after introducing evidence into your writing, you must demonstrate why and how this evidence supports your argument. You must explain the significance of the evidence and its function in your paper. What turns a fact or piece of information into evidence is the connection it has with a larger claim or argument: Evidence is always evidence for or against something, and you have to make that link clear.

 

What Is a Counterargument?

Remember that arguments are multi-sided. As you brainstorm and prepare to present your idea and your support for it, consider other sides of the issue. These other sides are counterarguments. Make a list of counterarguments as you work through the writing process, and use them to build your case – to widen your idea to include a valid counterargument, to explain how a counterargument might be defeated, to illustrate how a counterargument may not withstand the scrutiny your research has uncovered, and/or to show that you are aware of and have taken into account other possibilities.

For example, you might choose the issue of declawing cats and set up your search with the question should I have my indoor cat declawed? Your research, interviews, surveys, personal experiences might yield several angles on this question: Yes, it will save your furniture and your arms and ankles. No, it causes psychological issues for the cat. No, if the cat should get outside, he will be without defense. As a writer, be prepared to address alternate arguments and to include them to the extent that it will illustrate your reasoning.

Almost anything claimed in a paper can be refuted or challenged. Opposing points of view and arguments exist in every debate. It is smart to anticipate possible objections to your arguments – and to do so will make your arguments stronger. Another term for a counterargument is antithesis (i.e., the opposition to a thesis). To find possible counterarguments (and keep in mind there can be many counterpoints to one claim), ask the following questions:

• Could someone draw a different conclusion from the facts or examples you present?
• Could a reader question any of your assumptions or claims?
• Could a reader offer a different explanation of an issue?
• Is there any evidence out there that could weaken your position?

If the answer to any of these questions is yes, the next set of questions can help you respond to these potential objections:

Is it possible to concede the point of the opposition, but then challenge that point’s importance/usefulness?

• Can you offer an explanation of why a reader should question a piece of evidence or consider a different point of view?
• Can you explain how your position responds to any contradicting evidence?
• Can you put forward a different interpretation of evidence?

It may not seem likely at first, but clearly recognizing and addressing different sides of the argument, the ones that are not your own, can make your argument and paper stronger. By addressing the antithesis of your argument essay, you are showing your readers that you have carefully considered the issue and accept that there are often other ways to view the same thing.

You can use signal phrases in your paper to alert readers that you are about to present an objection. Consider using one of these phrases–or ones like them–at the beginning of a paragraph:

• Researchers have challenged these claims with…
• Critics argue that this view…
• Some readers may point to…

What Are More Complex Argument Structures?

So far you have seen that an argument consists of a conclusion and a premise (typically more than one). However, often arguments and explanations have a more complex structure than just a few premises that directly support the conclusion. For example, consider the following argument:

No one living in Pompeii could have survived the eruption of Mt. Vesuvius. The reason is simple: The lava was flowing too fast, and there was nowhere to go to escape it in time. Therefore, this account of the eruption, which claims to have been written by an eyewitness living in Pompeii, was not actually written by an eyewitness.

The main conclusion of this argument—the statement that depends on other statements as evidence but doesn’t itself provide any evidence for other statements—is

A. This account of the eruption of Mt. Vesuvius was not actually written by an eyewitness.

However, the argument’s structure is more complex than simply having a couple of premises that provide evidence directly for the conclusion. Rather, some statements provide evidence directly for the main conclusion, but some premise statements support other premise statements which then support the conclusion.

To determine the structure of an argument, you must determine which statements support which, using premise and conclusion indicators to help. For example, the passage above contains the phrase, “the reason is…” which is a premise indicator, and it also contains the conclusion indicator, “therefore.” That conclusion indicator helps identify the main conclusion, but the more important element to see is that statement A does not itself provide evidence or support for any of the other statements in the argument, which is the clearest reason statement A is the main conclusion of the argument. The next questions to answer are these: Which statement most directly supports A? What most directly supports A is

B. No one living in Pompeii could have survived the eruption of Mt. Vesuvius.

However, there is also a reason offered in support of B. That reason is the following:

C. The lava from Mt. Vesuvius was flowing too fast, and there was nowhere for someone living in Pompeii to go to escape it in time.

So the main conclusion (A) is directly supported by B, and B is supported by C.  Since B acts as a premise for the main conclusion but is also itself the conclusion of further premises, B is classified as an intermediate conclusion. What you should recognize here is that one and the same statement can act as both a premise and a conclusion. Statement B is a premise that supports the main conclusion (A), but it is also itself a conclusion that follows from C. Here is how to put this complex argument into standard form (using numbers this time, as is typical for diagramming arguments):

1. The lava from Mt. Vesuvius was flowing too fast, and there was nowhere for someone living in Pompeii to go to escape it in time.
2. Therefore, no one living in Pompeii could have survived the eruption of Mt. Vesuvius. (from 1)
3. Therefore, this account of the eruption of Mt. Vesuvius was not actually written by an eyewitness. (from 2)

Notice that at the end of statement 2 is a written indicator in parentheses (from 1), and, likewise, at the end of statement 3 is another indicator (from 2). From 1 is a shorthand way of saying, “this statement follows logically from statement 1.” Use this convention as a way to keep track of an argument’s structure. It may also help to think about the structure of an argument spatially, as the figure below shows:

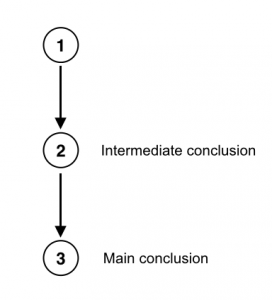
The main argument here (from 2 to 3) contains a subargument, in this case, the argument from 1 (a premise) to 2 (the intermediate conclusion). A subargument, as the term suggests, is a part of an argument that provides indirect support for the main argument. The main argument is simply the argument whose conclusion is the main conclusion.

Another type of structure that arguments can have is when two or more premises provide direct but independent support for the conclusion. Here is an example of an argument with that structure:

Wanda rode her bike to work today because when she arrived at work she had her right pant leg rolled up, which cyclists do to keep their pants legs from getting caught in the chain. Moreover, our co-worker, Bob, who works in accounting, saw her riding towards work at 7:45 a.m.

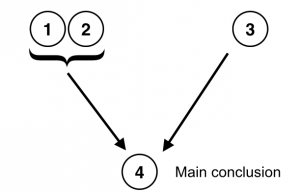
The conclusion of this argument is “Wanda rode her bike to work today”; two premises provide independent support for it: the fact that Wanda had her pant leg cuffed and the fact that Bob saw her riding her bike. Here is the argument in standard form:

1. Wanda arrived at work with her right pant leg rolled up.
2. Cyclists often roll up their right pant leg.
3. Bob saw Wanda riding her bike towards work at 7:45.
4. Therefore, Wanda rode her bike to work today. (from 1-2, 3 independently)

Again, notice that next to statement 4 of the argument is an indicator of how each part of the argument relates to the main conclusion. In this case, to avoid any ambiguity, you can see that the support for the conclusion comes independently from statements 1 and 2, on the one hand, and from statement 3, on the other hand. It is important to point out that an argument or subargument can be supported by one or more premises, the case in this argument because the main conclusion (4) is supported jointly by 1 and 2, and singly by 3. As before, we can represent the structure of this argument spatially, as the figure below shows:

 

There are endless argument structures that can be generated from a few simple patterns. At this point, it is important to understand that arguments can have different structures and that some arguments will be more complex than others. Determining the structure of complex arguments is a skill that takes some time to master, rather like simplifying equations in math. Even so, it may help to remember that any argument structure ultimately traces back to some combination of premises, intermediate arguments, and a main conclusion.

 

 

 

 

 

CC Licensed Content, Shared Previously

About Writing: A Guide, Robin Jeffrey, CC-BY.

A Concise Introduction to Logic, Craig DeLancey, CC-BY-NC-SA.

English 112: College Composition II,  Lumen Learning, CC-BY-SA.

English Composition 1,  Lumen Learning,  CC-BY-SA.

Frameworks for Academic Writing,  Stephen Poulter, CC-BY-NC-SA.

Introduction to Logic and Critical Thinking,  Matthew J. Van Cleave, CC-BY.

Methods of Discovery, Pavel Zemilanski,  CC-BY-NC-SA.

Writing for Success, CC-BY-NC-SA.

Writing in College: From Competence to Excellence,  Amy Guptill, CC-BY-NC-SA.

 

Image Credits

Figure 3.1 “Opinion vs Argument,” by Kalyca Schultz, Virginia Western Community College,  derivative image from original by ijmaki, pixabay, CC-0.

Figure 3.2 “Argument Diagram,” Virginia Western Community College, derivative image using “Thin Brace Down,” by pathoschild, Wikimedia, CC-BY-SA 3.0.

Figure 3.3 “Common Premise Indicators,” by Kalyca Schultz, Virginia Western Community College, CC-0.

Figure 3.4 “Common Conclusion Indicators,” by Kalyca Schultz, Virginia Western Community College, CC-0.

Figure 3.5 Untitled, by Matthew Van Cleave, from Introduction to Logic and Critical Thinking, CC-BY.

Figure 3.6 Untitled, by Matthew Van Cleave, from Introduction to Logic and Critical Thinking ,  CC-BY.