5 Reducing Error in Quantum Computing with Improved Circuit Design Methods
Alexander H. Jones, Howard Community College
Zobia Khan, University of Maryland, Baltimore County
Mentored by: Alex M. Barr, Ph.D.
Abstract
Using IBM’s Quantum Experience platform, we compare the accuracy of two different implementations of a half adder circuit on IBM’s quantum computers. We set out to show that a system of gates can perform the same logic function while reducing the error introduced to the algorithm. We find that the reduced number of Controlled-Not gates that compose the improved AND (QAND) gate set compared to the standard Toffoli AND gate results in significantly less error. We propose that the QAND gate set, composed of two Controlled-Hadamard gates with a Controlled Pauli-Z gate in between, can often provide more accurate results than a Toffoli gate in quantum algorithms.
Introduction
Classical computers, such as the device you are likely using to read this, carry out tasks by operating on internal components that represent binary digits, commonly known as bits. Classical bits are always in either a low (|0⟩) or high (|1⟩) state, other than the almost instantaneous transition between them when they react to an electrical voltage or current pulse that triggers at a defined threshold. Quantum computers are machines that perform operations on their respective components, known as qubits. These qubits can be represented in different fashions, depending on the quantum machine architecture: by the spin of an electron, the polarization of a photon, or in the IBM Quantum Experience machines, the direction of current in small superconducting current loops.
An essential difference between qubits and classical bits is that a qubit can exist in a superposition of both states |0⟩ and |1⟩ concurrently until it is observed or interacted with to measure its state [1]. Once measured, a qubit “collapses” into either state |0⟩ or state |1⟩. The ability of qubits to exist in a superposition of |0⟩ and |1⟩ gives quantum computers the potential to compute solutions that would otherwise not be possible or take several lifetimes for classical computers to perform. Potential uses for quantum computing include decrypting modern secure-encryption algorithms, decreasing runtime of unstructured search algorithms, and increasing the speed of linear algebra-intensive calculations in machine learning programs [2-5]. These applications, while not feasible with current quantum computers, present opportunities for great advancement. The potential of quantum computers to revolutionize the fields of computing and information science has led to significant investment in both research and educating a quantum-literate workforce [6].
Quantum computing technology is still in its relative infancy and faces issues stemming from susceptibility to noise and error introduced by the hardware used to sustain and perform operations on the qubits. Quantum error correction codes provide a potential solution, but these correction codes are not feasible on modern machines as they require tens of qubits just to maintain even one fault-tolerant qubit and current quantum computers contain fewer than 100 qubits total [7]. We set out to reduce the error in quantum algorithm results through the use of improved programming methods. In particular, we seek to improve the Boolean AND function in a half adder algorithm by replacing the common Toffoli gate with a collection of simpler gates that achieve the same Boolean results [5]. Throughout this paper, we will refer to this alternative implementation of the AND function as the “QAND”, for Quantum AND.
The half adder is a computational circuit that adds two bits/qubits to output a sum and carry bit-value. Combining two half adder circuits creates a full adder, a circuit often used in a sequential fashion to compute the addition of any two binary numbers. These circuits are foundational to computational operations and in lossy compression algorithms [8]. By improving the efficacy of quantum half adder circuits, the stability of larger algorithms which depend on the half and the full adder will consequently increase. To design and execute our experiments, we use the online Quantum Experience platform provided by IBM which allows users around the world to execute algorithms on any of IBM’s eight publicly available quantum computers. The quantum algorithms are designed and submitted to Quantum Experience using the Qiskit library for the Python programming language [5, 9, 10]. These tools provide access to those interested in quantum computing, by lowering the barrier of entry for those in computer science and similar fields by reducing the depth of quantum physics knowledge required to engage in the development of quantum applications [11].
In the following sections, we compare the accuracy of a basic half adder implementation to a half adder that implements the QAND gate system and a more intentional qubit selection based on the qubit connectivity of the underlying quantum computer. In support of these overall results, we independently measure the accuracy of a Toffoli gate against the QAND gate system, the amount of error introduced by increasing quantities of different gate operations, and the error associated with measuring a qubit state. We discuss the importance of qubit connectivity and show how careful selection of the qubits used in algorithm design can increase the efficacy of the algorithm. In the end, we summarize these design principles and consider their applications to various quantum algorithms.
Two Designs for a Half Adder
A half adder takes two input bit values, A and B, to compute one sum output and a carry output. The sum and carry combine in a bit string where the sum is the least significant bit, and the carry is the most significant bit: |B⟩+ |A⟩= |Carry Sum⟩. Half adders used in a classical computer consist of XOR and AND gates. These circuits are frequently found in calculators, computers, and digital measurement devices.
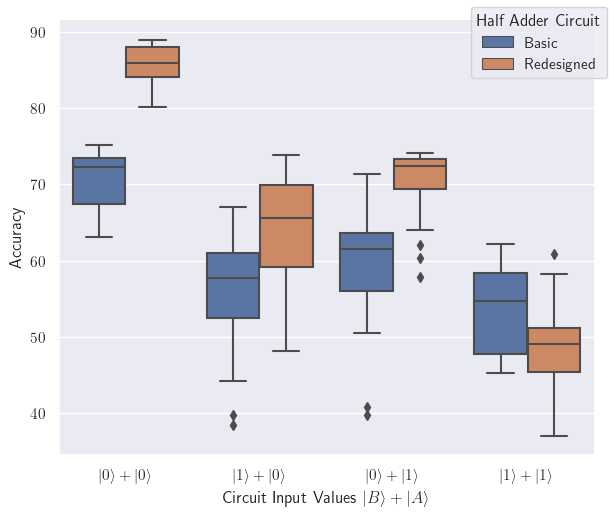
In quantum computing, algorithms are typically run many times with each run referred to as a “shot”. Throughout this paper, we define the accuracy of an executed quantum algorithm as the number of shots that were measured to have the expected outcome based on the classical and logical functions the quantum circuit represents divided by the total number of shots. We report the accuracy as a percentage between 0 and 100. Figure 1 shows the accuracy for both the basic and redesigned half adder, for all four possible input combinations. Each input combination was run for 20 trials, and each trial executed 8192 shots. Each half adder design was thus executed on the ibmq_quito quantum computer a total of 20 x 8192 = 163,840 times for each of the four input combinations. Collecting this data can take anywhere from a few hours to almost a week’s time, depending on how many users are queued to execute their experiments on IBM’s quantum computers at the time.
Both of the half adder algorithms we tested are deterministic. The variation in the output from one shot to the next in our experiments results is due to experimental noise and hardware error, not the probabilistic nature of quantum mechanics. The half adder circuit thus provides a useful context for exploring sources of error and methods for reducing said error in quantum algorithm design.
In Figure 1, we compare the accuracy of two half adder algorithms, one that uses a basic circuit design that does not attempt to minimize error, and a redesigned circuit that attempts to account for and minimize different sources of error. Each algorithm was tested with all four possible input state combinations: |0⟩+|0⟩, |0⟩+|1⟩, |1⟩+|0⟩, and |1⟩+|1⟩. We observe that in all but one input case, the redesigned half adder is more accurate than the basic half adder circuit. For |00⟩, |01⟩, and |10⟩ input states our modified half adder is more accurate by an average of 11.27%. Interestingly, for the input state |11⟩, the basic half adder is more accurate than the redesign at producing the expected output. Across all four input states, the redesigned half adder is more accurate by 7.22% than the basic half adder.

Both of these circuits were run on the 5-qubit IBM Quantum Falcon processor ibmq_quito v1.0.10, which has qubits connected in a T-shaped fashion.
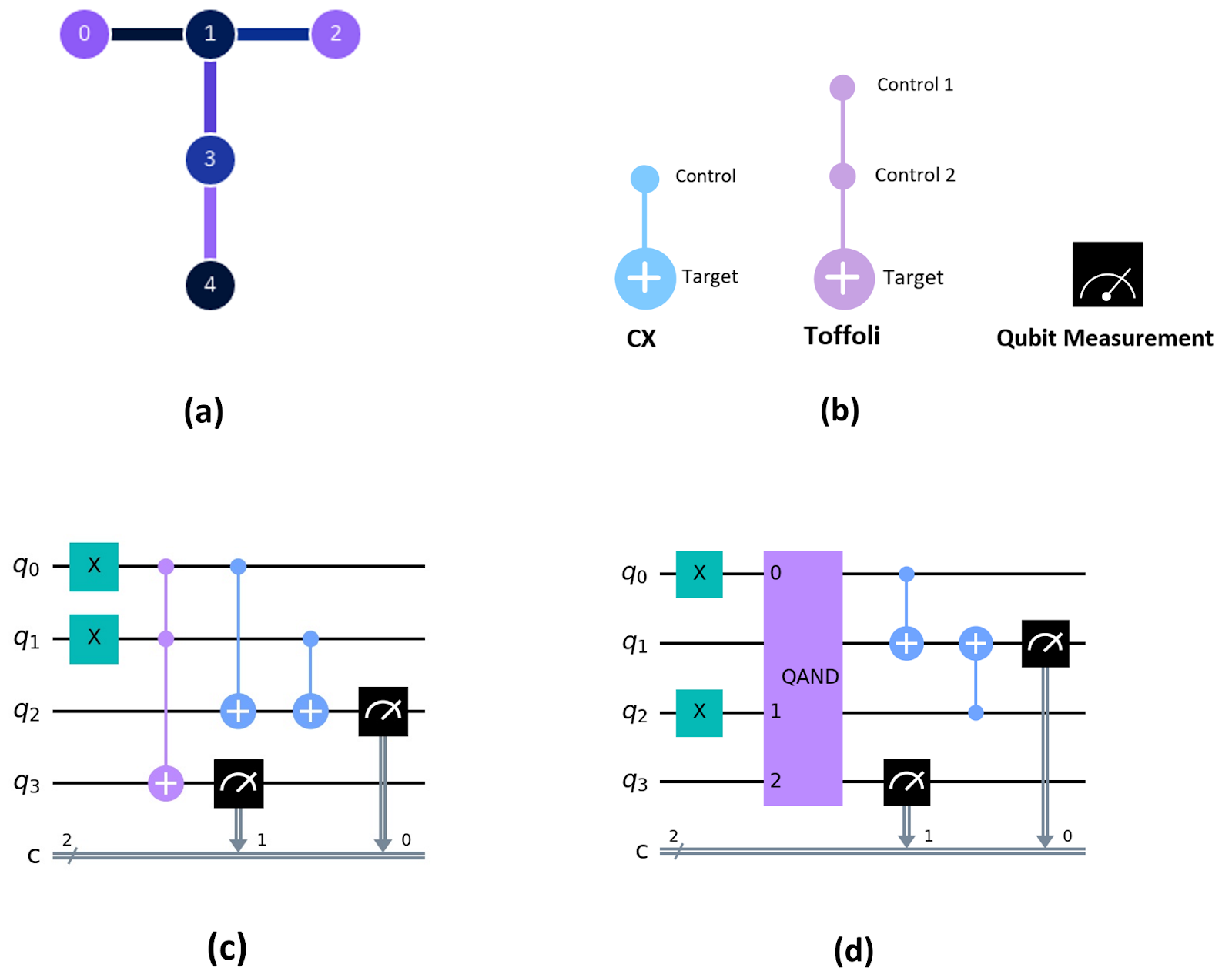
In the basic quantum half adder, qubit0 and qubit1 represent the inputs A and B that we wish to add. All qubits begin in state |0⟩ and we apply Pauli-X (X) gates as needed to set |q0⟩ and/or |q1⟩ to |1⟩ for the desired input state. The circuit shown in Figure 2(c) represents input |1⟩+|1⟩. Once the input is set, the basic half adder consists of a pair of Controlled-NOT (CX) gates that perform the sum computation and assign the result to qubit2, and a Toffoli gate that performs the carry operation and assigns the result to qubit3 [5]. The output is then obtained by measuring qubit2 and qubit3 and writing those results to classical computer memory represented by line c in the diagram.
Similar to the basic half adder, the redesigned circuit in Figure 2(d) begins by applying X gates as needed to set the desired input values. In the redesign, we select qubit0 and qubit2 as the input qubits based on the T-shaped qubit connectivity of the ibmq_quito machine on which the half adder is being executed. This ensures that both input qubits can interact with the QAND gate set which implements the carry operation. The sum operation is then implemented using a pair of CX gates. Executing the carry operation before the sum allows the input qubits to interact directly with the QAND gate set which is the most complicated portion of the circuit. The output of the half adder is obtained by measuring qubit1 which represents the sum digit and measuring qubit3 which represents the carry digit and writing the results to classical computer memory.
QAND vs Toffoli
A significant difference between the half adder algorithms in Figure 2 is how the carry operation is implemented. In classical computing, the carry operation is implemented using an AND gate: a digital logic gate that outputs a 1, if and only if both of the inputs are 1. In quantum computing, the Toffoli gate is often used to perform AND operations. The Toffoli gate is denoted by two filled circles connected to a third circle with a + inside. The qubit lines with the filled circles are the inputs to the AND operation and the qubit with the + becomes the output of the AND operation. Despite the simple notation, implementing the Toffoli gate on IBM’s quantum computers actually involves applying a sequence of less complex single and multi-qubit gates as shown in Figure 3. The details of the individual H and T gates are not important for the current discussion. Of central importance is the fact that implementing the Toffoli gate involves nine single-qubit gates and six two-qubit CX gates.
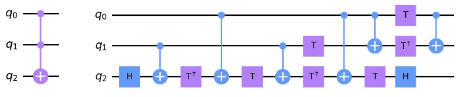
The QAND gate set performs the same logical function as the Toffoli gate. It consists of a controlled Hadamard gate (CH), a controlled Pauli-Z gate (CZ), and another CH gate [5]. The CH and CZ gates are implemented on IBM’s quantum computers using the sequence of gates shown in Figure 4. Comparing the full gate sequences for Toffoli and QAND, we see that while the QAND gate set is composed of 17 total gates compared to the 15 total gates of a Toffoli composition, the QAND uses half as many of the two-qubit CX gates.

Figure 5 compares the Toffoli and QAND implementations of the AND operation, showing their accuracy for the four different possible inputs. To calculate accuracy, we define our expected output as the logical AND operation, for which the output is |0⟩ unless both inputs are |1⟩. Each implementation and input was executed for 20 trials of 8192 shots each.
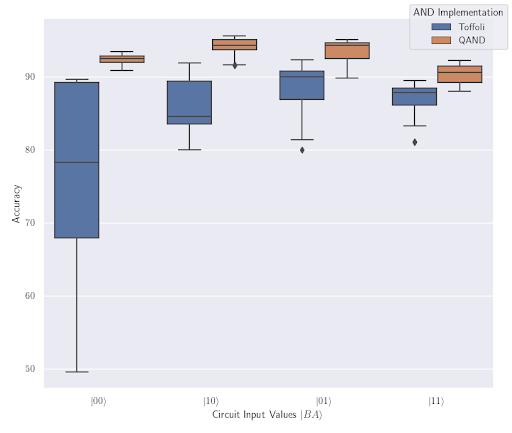

We observe two notable differences between the Toffoli and QAND results. First, we observe that the QAND has an overall higher average accuracy. Secondly, we observe that the QAND has a tighter distribution of results, indicating that the output is more predictable. These results suggest that the number of CX gates has a larger impact on the accuracy than the number of single qubit gates.
Gate Error
In order to compare the impact that different gates have on accuracy, we ran strings of single-qubit Hadamard (H) and Pauli-X (X) gates and the two-qubit CX gates on the now-retired machine ibmq_vigo v1.3.6. We initialized the qubits to state |1⟩ then applied a single gate type repeatedly before measuring qubit. By repeating this process for progressively longer gate sequences and comparing the measured results to the expected output we obtain a measure of the error associated with each gate type.
The H gate is one of the most essential quantum gates, as it places the qubit in superposition, a quantum state that is a linear combination of states |0⟩ and |1⟩. The X gate is similar to a logical NOT gate, as an X gate inverts the state |0⟩ to |1⟩ and vice versa. The H and X gates are common single qubit gates and their errors should be representative of single qubit gate error. The CX gate involves two qubits: a control qubit and a target qubit. If the control qubit is in state |1⟩, an X gate will operate on the target qubit. If the control qubit is in state |0⟩ then the target qubit is not operated on.
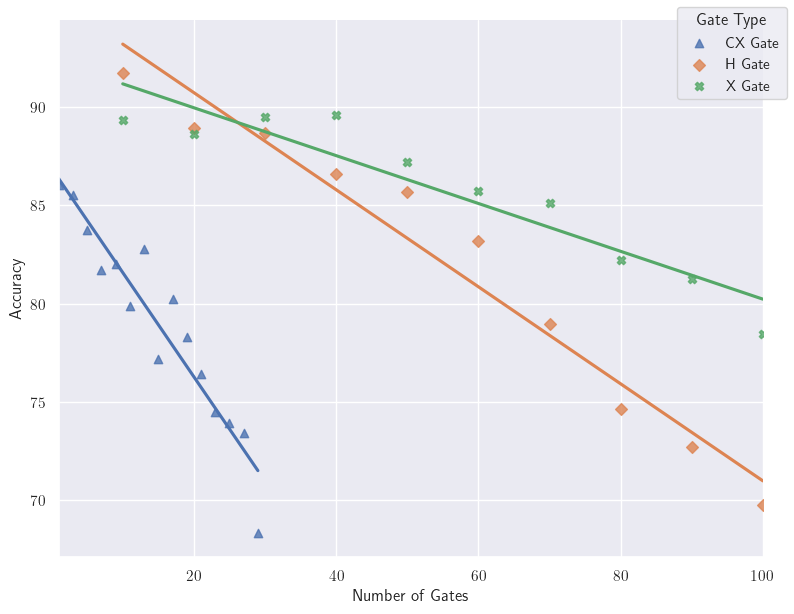
Figure 6 shows a graph of the Accuracy vs Number of Gates. As we increase the number of gates being applied the accuracy of the output decreases for each gate. We observe that the accuracy decreases faster with H gates as compared to X gates. The reason this makes sense is because we are creating a state of superposition with the H gate whereas the X gate is just inverting the qubit’s state. The H gate is more prone to error because while the qubit is in the superposition state there are chances that due to the hardware on which our circuit is running the qubit could “collapse” into state |0⟩ or |1⟩ before the algorithm finishes running. Furthermore, the accuracy decreases more than twice as quickly when applying CX gates compared to H and X gates. A CX gate is more vulnerable to error as compared to the single qubit H and X gates.
Figures 3 and 4 showed the gate composition of Toffoli and QAND, respectively. The QAND gate composition involves more total gates compared to the Toffoli gate, however, the Toffoli gate is composed of more CX gates compared to the QAND gate set. The higher accuracy of the QAND is attributable to being constructed from fewer of the two-qubit CX gates than the Toffoli. By replacing the Toffoli gate in the half adder with the QAND gate we reduce the number of CX gates and we can expect a higher overall accuracy.
Qubit Connectivity
The diagrams in Figure 7 represent various qubit connectivity couplings of some machines available through IBM’s Quantum Experience. The connectivity of a quantum computer refers to the pairs of qubits that support two-qubit gate operations between them [9]. This physical feature determines the operations possible on the machine. A multi-qubit gate operation like a CX requires the control and target qubits to be connected.
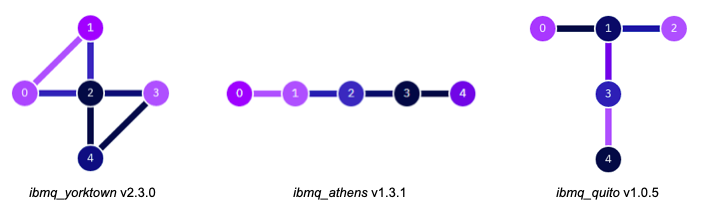
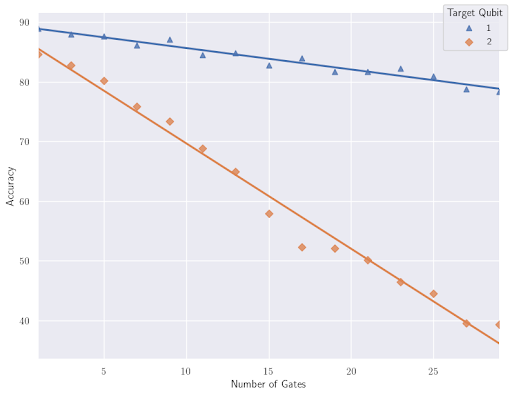
In the previous section, we showed that the accuracy decreases linearly as the number of gates applied increases, and that this decrease is most pronounced for CX gates. We now examine this relationship further by measuring the decrease in accuracy when CX gates are applied to connected qubits vs non-connected qubits. Figure 8 compares accuracy vs number of CX gates applied for two different pairs of qubits on the ibmq_quito machine. Qubit0 was used as the control qubit in both cases with either qubit1 or qubit2 being used as the target qubit. The rate of decrease in accuracy is approximately five times greater for non-connected qubits (q0-q2) compared to connected qubits (q0-q1). This highlights the importance of qubit selection in implementing the QAND in a half adder algorithm, and moreover, in all quantum computing algorithms. In Figure 2, the input qubits for the redesigned half adder were selected based on the ibmq_quito topology diagram to minimize the use of CX gates between non-connected qubits.
While the connectivity of qubits is fixed for a given machine, it is possible to swap the quantum states of two qubits by applying a sequence of three CX gates with alternating control and target positions [5]. A CX operation between qubit0 and qubit2 on ibmq_quito thus requires a total of four CX gates: three to swap the states of qubit2 and qubit1 and fourth to execute the CX between between qubit0 and the quantum state now residing in qubit1. This is why the accuracy decreases approximately four to five times as fast using qubit2 as the target in Figure 8 compared to using qubit1 as the target. These additional CX gates required to swap the states of qubit2 and qubit1 are executed by Qiskit automatically.
Because the additional CX gates required in order to execute a CX operation between non-connected qubits have a significant impact on an algorithm’s accuracy, Qiskit’s default mode will automatically change qubit assignments in a circuit to try to minimize operations between non-connected qubits. In order to measure the impact of qubit connectivity directly as in Figure 8, a user should specify an optimization level of zero so that Qiskit will follow your explicit qubit assignments. The code used for these measurements and others is available at [12].
Measurement Error
In addition to gate error, there is also error associated with the process of measuring the qubits to obtain the results of a quantum algorithm. During measurement, possibility of error exists in the form of a qubit state |0⟩ being measured as a |1⟩ or vice versa or in the measured result being perturbed before being returned to the user. It has been previously noted that the measurement of different states does not occur equally erroneously, with state |1⟩ being more prone to measurement error than state |0⟩ [13]. Both the basic half adder design and the redesign are equally susceptible to measurement error.
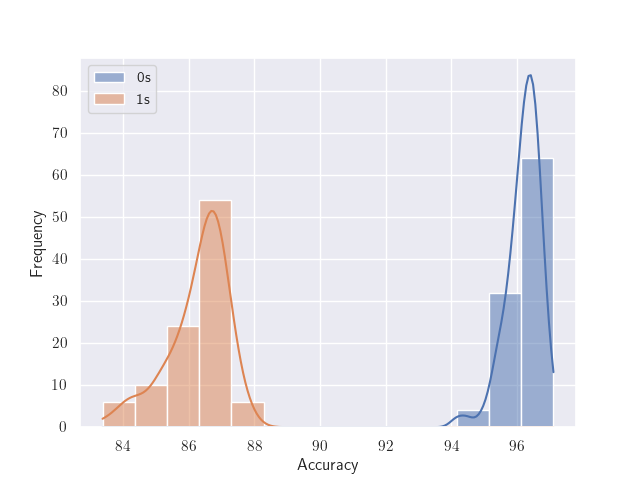
Figure 9 demonstrates the quantifiable difference in accuracy between measuring a qubit in state |0⟩ and in state |1⟩. All five qubits for the quantum computer were initialized to state |0⟩ or state |1⟩ and then measured for 100 trials of 8192 shots for each initial state. For each trial, we record the percentage of shots for which all five qubits are measured to be in the state to which they were initialized. The results show that the hardware interaction of measuring the higher energy |1⟩ state of a qubit is more error prone than measuring the lower energy |0⟩ state. We also see that the measurement accuracy for state |1⟩ has a greater standard deviation than the measurement accuracy of state |0⟩. This information was taken into account when measuring gate error in Figures 6 and 8 as we selected experimental results where the number of gates applied was odd, always resulting in an expected output of |1⟩ to maintain consistency with the measurement error introduced.
The lower measurement accuracy for state |1⟩ can be partially explained by the qubit being measured experiencing decoherency, or the loss of quantum coherence. As qubits are extremely sensitive objects, they naturally decay from their higher energy |1⟩ state to their lower energy |0⟩ state in a matter of microseconds. Seeing as quantum mechanics is fundamentally probabilistic, inherently so will be the measurement of a binary state. This is compounded by the fact that these machines have physical imperfections and will introduce some amount of experimental error when measuring a qubit state. We are aware of the existence of these factors in our experiment design, but we did not attempt to address them as it was not the focus of our investigation.
Conclusions
As we focus on the results of the half adder redesign, we conclude that the new design increases the accuracy by an average of 7.22% compared to the basic design. The increased accuracy is largely due to the use of the QAND gate-set in place of the Toffoli gate. Comparing only the logical AND function of the Toffoli gate vs the QAND gate set showed a mean improvement of 8.5% across all inputs. We assert that this improvement is brought about by the reduced number of CX gates required to implement QAND. As demonstrated in Figure 6, increasing the number of either single or multi-qubit gates introduces hardware noise presenting itself as error caused by the microwave pulses that apply the gates. The introduced error is most notable in the two-qubit CX gate, which is applied six times in the Toffoli gate compared to only three times in QAND.
Additionally, we conclude that well-designed qubit assignments can have a significant effect on the overall performance of an algorithm. This concept is exceptionally important in algorithms that use multi-qubit gates like the CX, CZ, CH, and Toffoli gates. Implementing CX gates between non-connected qubits can reduce the accuracy by a factor of four to five compared to CX gates between connected qubits. It is also important to note that different quantum computers have different qubit topologies. An algorithm with many multi-qubit gates may achieve the greatest accuracy on a quantum computer with a more connected topology even if the individual gate errors are slightly higher on that machine.
We propose that using the QAND gate set in algorithms that utilize a logical AND function and explicitly considering qubit connectivity will increase the accuracy of deterministic algorithms, or algorithms that require some portion of deterministic computation for an otherwise probabilistic computation. These design principles provide an intermediate tool for the mitigation of error in quantum algorithms until machines with the necessary numbers of qubits to implement Error Correction Codes for fault-tolerant qubits are developed.
One machine available to users on the Quantum Experience platform, ibmq_melbourne v2.3.9, has a Canary Quantum processor with 15 qubits provides enough qubits to implement a full adder algorithm. Investigating the effects of the QAND in a full adder would be the next step to take in relation to our experiments, as a full adder is composed of two half adders. We believe that it would have a positive net effect on the performance of the more complex circuit. A related, but non-linear direction to pursue, involves using the QAND gate-set in a decoder circuit as a component of autoencoder machine learning algorithms and neural networks [14, 15, 16].
Additionally, the accuracy of the QAND in scenarios that require the use of non-connected qubits, could be explored to evaluate if the QAND is still an improvement over the Toffoli. Also unaccounted for in our experiment is how gate error and measurement error vary from qubit to qubit. The ideal algorithm design procedure would account not only for qubit connectivity as demonstrated here, but also variation in error introduced by gates and measurement for each qubit used in the circuit.
Acknowledgements
We acknowledge the use of IBM Quantum Services for this work. The views expressed are those of the authors, and do not reflect the official policy or position of IBM or the IBM Quantum team.
Contacts: jones51595@gmail.com, zkhan6@umbc.edu, abarr@howardcc.edu
References
[1] Z. Weinersmith, “Saturday Morning Breakfast Cereal – The Talk,” RSS, 14-Dec-2016. [Online]. Available: https://www.smbc-comics.com/comic/the-talk-3. [Accessed: 26-Feb-2021].
[2] A. G. Fowler, S. J. Devitt, and L. C. L. Hollenberg. 2004. Implementation of Shor’s algorithm on a linear nearest neighbour qubit array. Quantum Info. Comput. 4, 4 (July 2004), 237–251.
[3] Grover, Lov K.. “A Fast Quantum Mechanical Algorithm for Database Search.” . In Proceedings of the Twenty-Eighth Annual ACM Symposium on Theory of Computing (pp. 212–219). Association for Computing Machinery, 1996.
[4] Harrow, Aram W., Avinatan, Hassidim, and Seth, Lloyd. “Quantum Algorithm for Linear Systems of Equations”.Phys. Rev. Lett. 103 (2009): 150502.
[5] A. Asfaw, et al. “Learn Quantum Computation using Qiskit,” 2020.
[6] Fox, Michael F. J., Benjamin M., Zwickl, and H. J., Lewandowski. “Preparing for the quantum revolution: What is the role of higher education?”. Physical Review Physics Education Research 16, no.2 (2020).
[7] Tannu, Swamit S., and Moinuddin K., Qureshi. “Not All Qubits Are Created Equal: A Case for Variability-Aware Policies for NISQ-Era Quantum Computers.”. In Proceedings of the Twenty-Fourth International Conference on Architectural Support for Programming Languages and Operating Systems (pp. 987–999). Association for Computing Machinery, 2019.
[8] Binary adder and binary addition using ex-or gates. (2018, September 20). Retrieved April 01, 2021, from https://www.electronics-tutorials.ws/combination/comb_7.html
[9] IBM Quantum. https://quantum-computing.ibm.com/, 2021
[10] Abraham, Héctor, et al. Qiskit: An Open-Source Framework for Quantum Computing. 2019, doi:10.5281
[11] Mermin, N. David. “From Cbits to Qbits: Teaching computer scientists quantum mechanics”. American Journal of Physics 71, no.1 (2003): 23–30.
[12] Jones A., et al. (2021) Reducing Error With QAND, Reducing-Error-With-QAND.ipynb, https://github.com/henriksound-bit/Reducing-Error-in-Quantum-Computing-with-Improved-Circuit-Design-Methods
[13] Tannu, Swamit S., and Moinuddin K., Qureshi. “Mitigating Measurement Errors in Quantum Computers by Exploiting State-Dependent Bias.”. In Proceedings of the 52nd Annual IEEE/ACM International Symposium on Microarchitecture (pp. 279–290). Association for Computing Machinery, 2019.
[14] Types of binary decoders,applications. (2017, December 24). Retrieved April 01, 2021, from https://www.electronicshub.org/binary-decoder/
[15] Dertat, A. (2017, October 08). Applied deep learning – Part 3: Autoencoders. Retrieved April 01, 2021, from https://towardsdatascience.com/applied-deep-learning-part-3-autoencoders-1c083af4d798#ad4f
[16] Lamata, L., Alvarez-Rodriguez, U., Martín-Guerrero, J., Sanz, M., & Solano, E. (2018). Quantum autoencoders via quantum adders with genetic algorithms. Quantum Science and Technology, 4(1), 014007.