Equivalence Classes of Complex Numbers Modulo a Natural Number
Jonathan Kraus, Howard Community College
David Ryan Johnson, Howard Community College, 2019, Towson University
Mentored by Dr. Mike Long, Howard Community College
Abstract
Equivalence classes of natural numbers are sets of numbers that have a common characteristic. One well-known equivalence class involves the modulus operator, or the value of the remainder when a natural number is divided by “n,” which is also a natural number. For example, an equivalence class modulo 4, would be a set of numbers that have the same remainder when divided by 4. Since there are four possible remainders when dividing by 4, there would be four equivalence classes in this case. The question that emerges is what are the characteristics of equivalence classes of complex numbers modulo a natural number, “n”? In this project, we explore those mathematical characteristics that unfold in the equivalence classes and also the geometry of the classes in the complex plane. Further exploration of the geometry of the classes yielded intriguing, yet well-known, mathematical patterns. This leads to another question, what patterns exist in the geometric structures of the equivalence classes with complex numbers modulo n? We will describe those patterns and offer proof or rationale for the existence of the patterns.
Introduction
The complex numbers in mathematics are numbers that have the form a + bi with the “a” being the real part of the number and the “b” being the coefficient of the imaginary part “i” [1]. The “i” is the mathematical representation of the square root of negative one. When studying the algebra of the real numbers, the square root of negative one is undefined, but the complex numbers allow for the square root of negative one to be defined and, with algebra, the square root of any negative number can be defined. By defining the square root of negative one, equations that could not be solved over the real numbers can be solved.
The second part of this research involves equivalence classes. In elementary abstract algebra or discrete mathematics, one learns about the idea of mathematical equivalence classes. To begin defining an equivalence class (and equivalence relations), consider a set of elements and subsets of those elements that have a common characteristic or relationship [2, 3]. The equivalence relation mod n where “n” is a positive integer or natural number, is the important part of this paper. To better understand this notion, let’s consider the set of positive integers {1, 2, 3, 4, 5, 6, 7, 8, 9} and the equivalence relation mod 3. Another way of thinking about this is that the difference of any two elements in the equivalence classes is a multiple of three. More formally, x – y is equal to a multiple of three where x and y are any random elements of the subset. In order to be an equivalence relation on a set, three properties must exist: reflexive, or in this case x – x has to be divisible by three; symmetric, or in this case if x – y is divisible by three then y – x must be divisible by three; and transitive, or in this case if x – y and y – z are divisible by three, then x – z must be divisible by three. (Here z is also an element of the original set.) It can be shown with a simple proof that mod 3 is indeed an equivalence relation.
Proof that mod 3 is an equivalence relation
First, it must be shown that the reflexive property holds. So every element has to be related to itself or x – x has to be divisible by three, where x is a random element of the set being considered. Since x – x = 0, which is also equal to three times 0, x – x is divisible by three. This shows the reflexive property holds. Next, it must be shown that the symmetric property holds. This means that if x is related to y, where x and y are random elements of the set being considered, then y is related to x or, equivalently, if x – y is divisible by three then y – x must be as well. We start by saying that x – y is divisible by three and so there exists an integer, call it k, such that x – y = 3k. If both sides are multiplied by negative one then the equation becomes -x + y = -3k which can be rewritten as y – x = 3(-k). The (-k) will still be an integer and so x is divisible by three. This shows the symmetric property holds. Finally, it must be shown that the transitive property holds. This means that if x is related to y and y is related to z then x is related to z, where x, y, and z are random elements of the set being considered or if x – y and y – z are divisible by three then x – z is divisible by three. We start by saying that x – y and y – z are divisible by three and so there exists integers j and k such that x – y = 3k and y – z = 3j. Then if x – y and y – z are added together (x – y) + (y – z) = 3k +3j and then x – z = 3(k + j), where k + j is an integer. Therefore x – z is a multiple of three.
Another way to think about this same relation is which elements in the original set {1, 2, 3, 4, 5, 6, 7, 8, 9} have the same remainder when divided by three. So one equivalence class would be the elements of the original set that have a remainder of zero when divided by three {3, 6, 9}. Another class would be the elements of the original set that have a remainder of one when divided by three {1, 4, 7}. And the final class would be the elements of the original set that have a remainder of two when divided by three {2, 5, 8}. It should also be noted that this equivalence relation forms the partition of the original set. In other words, the three subsets have no common elements and when the three subsets are put together, they form the entire original set.
These two ideas, complex numbers and equivalence classes, lead to the research here.
First Research Question
What do the equivalence classes of the complex numbers modulo n or mod n (where n is a natural number) with integer values for the real and imaginary part, look like algebraically, but more important, what do they look like geometrically? Two immediate considerations emerge:
- First, a definition must be established for complex numbers modulo n and in this case the conventional definition that both the real and imaginary parts will be independently evaluated modulo n or mod n, will be used.
- Second, the geometry will require two dimensions in order to account for the real and imaginary parts when graphing the complex numbers. This second consideration leads to a major part of the research.
In order to understand the idea of the equivalence classes, a table of complex numbers with integral values for the real and imaginary parts will be examined mod 3. This means looking at the remainders when the real and imaginary parts of the complex number are independently divided by three. Negative numbers need not be addressed here as we are simply looking at the remainders when dividing by “n.” Table 1 shows this.
| Complex Number | Complex Number mod 3 |
Complex Number | Complex Number mod 3 |
| 0 + 0i | 0 + 0i | 3 + 0i | 0 + 0i |
| 0 + 1i | 0 + 1i | 3 + 1i | 0 + 1i |
| 0 + 2i | 0 + 2i | 3 + 2i | 0 + 2i |
| 0 + 3i | 0 + 0i | 3 + 3i | 0 + 0i |
| 0 + 4i | 0 + 1i | 3 + 4i | 0 + 1i |
| 0 + 5i | 0 + 2i | 3 + 5i | 0 + 2i |
| 0 + 6i | 0 + 0i | 3 + 6i | 0 + 0i |
| 0 + 7i | 0 + 1i | 3 + 7i | 0 + 1i |
| 0 + 8i | 0 + 2i | 3 + 8i | 0 + 2i |
| 1 + 0i | 1 + 0i | 4 + 0i | 1 + 0i |
| 1 + 1i | 1 + 1i | 4 + 1i | 1 + 1i |
| 1 + 2i | 1 + 2i | 4 + 2i | 1 + 2i |
| 1 + 3i | 1 + 0i | 4 + 3i | 1 + 0i |
| 1 + 4i | 1 + 1i | 4 + 4i | 1 + 1i |
| 1 + 5i | 1 + 2i | 4 + 5i | 1 + 2i |
| 1 + 6i | 1 + 0i | 4 + 6i | 1 + 0i |
| 1 + 7i | 1 + 1i | 4 + 7i | 1 + 1i |
| 1 + 8i | 1 + 2i | 4 + 8i | 1 + 2i |
| 2 + 0i | 2 + 0i | 5 + 0i | 2 + 0i |
| 2 + 1i | 2 + 1i | 5 + 1i | 2 + 1i |
| 2 + 2i | 2 + 2i | 5 + 2i | 2 + 2i |
| 2 + 3i | 2 + 0i | 5 + 3i | 2 + 0i |
| 2 + 4i | 2 + 1i | 5 + 4i | 2 + 1i |
| 2 + 5i | 2 + 2i | 5 + 5i | 2 + 2i |
| 2 + 6i | 2 + 0i | 5 + 6i | 2 + 0i |
| 2 + 7i | 2 + 1i | 5 + 7i | 2 + 1i |
| 2 + 8i | 2 + 2i | 5 + 8i | 2 + 2i |
In this example of the equivalence relation mod 3, there are nine different equivalence classes that emerge and they are represented by the complex numbers in the “Complex Number mod 3” column. Let’s consider the equivalence class 1 + 2i to solidify this idea. The numbers highlighted all belong to the same equivalence class, 1 + 2i, since they all have the same remainders when the real and imaginary parts of the complex number are independently divided by three. The complex numbers within this equivalence class have the three properties already mentioned: reflexive, symmetric, and transitive and that is proved here for a generic complex number of the form a + bi.
Proof that mod 3 is an equivalence relation
First, it must be shown that the reflexive property holds. This means that a + bi needs to be related to itself or (a + bi) – (a + bi) has to be a multiple of three. (a + bi) – (a + bi) = 0 = 3 x 0. Zero is a multiple of three, and therefore a + bi is related to itself. This shows the reflexive property exists. Next, it must be shown that the symmetric property holds. This means that a + bi and c + di need to be symmetric or if (a + bi) – (c + di) is a multiple of three, then (c + di) – (a + bi) is also a multiple of three. Since (a + bi) – (c + di) is a multiple of three there exists an integer k such that (a + bi) – (c + di) = 3k. If both sides are multiplied by negative one then (-1)((a + bi) – (c + di)) = (-1)3k = 3(-k) = (c + di) – (a + bi). This shows the symmetric property exists. Finally, it must be shown that the transitive property holds. This means that a + bi, c + di, and f + gi need to be transitive. In other words, if (a + bi) – (c + di) is a multiple of three, and (c + di) – (f + gi) is a multiple of three, then (a + bi) – (f + gi) is a multiple of three. Since (a + bi) – (c + di) is a multiple of three and (c + di) – (f + gi) is a multiple of three, there exists integers j and k such that (a + bi) – (c + di) = 3k and (c + di) – (f + gi) = 3j. Now ((a + bi) – (c + di)) + ((c + di) – (f + gi)) = 3k + 3j = 3(k + j) = (a + bi) – (f + gi). This shows that (a + bi) – (f + gi) is a multiple of three. This shows that the transitive property exists and completes the proof.
What’s interesting to note is that there are nine equivalence classes, which happens to be a perfect square number, when considering the complex numbers mod 3. This makes sense because when dividing by three there are three possible remainders: 0, 1, and 2. Since we have to consider both real and complex (imaginary) parts, it is like considering the cross product of A and B where A is the possible remainders for the real part: 0, 1, and 2, and B is the possible remainders for the imaginary part: 0, 1, and 2. So there would be nine possibilities where the first coordinate of the ordered pair is the remainder for real part and the second is the remainder for the imaginary part mod 3: ![]() . This could be easily extended to the complex numbers, with integral values,
. This could be easily extended to the complex numbers, with integral values, ![]() , where n is a positive integer. And so in all cases, there would be
, where n is a positive integer. And so in all cases, there would be ![]() , or a square number of equivalence classes. Algebraically, we can say that the number of equivalence classes of the complex numbers with integral coefficients mod n, where n is a natural number, is a perfect square.
, or a square number of equivalence classes. Algebraically, we can say that the number of equivalence classes of the complex numbers with integral coefficients mod n, where n is a natural number, is a perfect square.
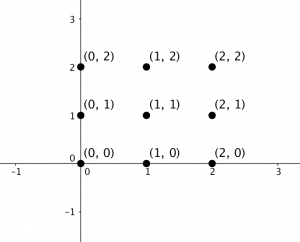
Now let’s move forward and investigate the geometry of these equivalence classes. Remember that the complex numbers require two dimensions to be represented graphically. Think of it as the x-axis and y-axis. The nine equivalence classes of the complex numbers mod 3 are graphically represented in Figure 1 below. The arrangement of the equivalence classes forms a square lattice, which seems fitting given that nine is a perfect square number. Again, this can be easily extended to mod n where the equivalence classes would form an ![]() square and with ordered pairs (real and imaginary parts) with values from zero to n – 1, where the zero to n – 1 show all of the possible remainders when the real and imaginary parts are divided by n. So geometrically, equivalence classes of the complex numbers with integral coefficients mod n, where n is a natural number, form square lattices.
square and with ordered pairs (real and imaginary parts) with values from zero to n – 1, where the zero to n – 1 show all of the possible remainders when the real and imaginary parts are divided by n. So geometrically, equivalence classes of the complex numbers with integral coefficients mod n, where n is a natural number, form square lattices.
Second Research Question
A second question involving the complex numbers and their equivalence classes emerged after exploring the basics of the geometry. Suppose that you consider a complex number involving integral real and imaginary parts and all possible positive and negative values for those real and imaginary parts. Is there anything unique that happens in the geometry? In order to begin answering this question we need to identify the real and imaginary parts of the complex number. For simplicity, “a” will be the real part and “b” will be the imaginary part. So the four complex numbers to be considered will be: a + bi, a – bi ,-a + bi, and -a – bi. Again, we want to consider each of these complex numbers mod n where n is a natural number or positive integer. And both the real and imaginary parts will be independently evaluated mod n as before. It turns out an interesting pattern emerges.
We will use the example ![]() along with the positive and negative combinations of the number as suggested above to begin to form a pattern:
along with the positive and negative combinations of the number as suggested above to begin to form a pattern:
![]()
![]()
We will also take all of the values to be positive in the equivalence classes. Again, negative numbers need not be addressed here as we are simply looking at the remainders when dividing by “n.” So in this example, a = 4 and b = 5 and n = 3. Figure 2 organizes this example for simplicity.
![]()
![]()
![]()
![]()
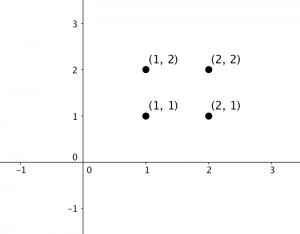
Figure 2: This shows the geometry that results from graphing the four complex numbers above mod 3.
A rather simple geometric figure emerges, a rectangle, and in this particular case it is a square. Figure 3 shows the graph of the results in Figure 2.
This notion can be generalized as seen below and in this generalization a rectangle again forms in all cases given the coordinates of the equivalence classes of the complex numbers, with integral real and imaginary parts, mod n. Figure 4 organizes this generalization for simplicity.
![]()
![]()
![]()
![]()
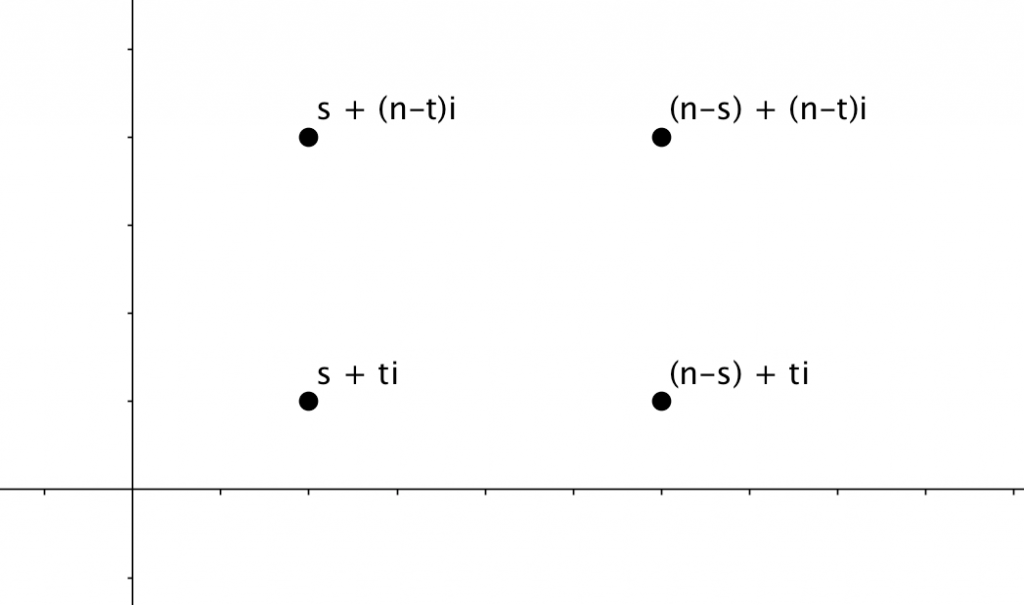
Figure 4: This shows the geometry that results from graphing the four generalized complex numbers above mod n.
Figure 5 shows the graph of the generalization in Figure 4.
Third Research Question
When looking at the geometry of these four complex numbers, (a + bi) mod n = s + ti, (a – bi) mod n = s + (n – t)i, (-a + bi) mod n = (n – s) + ti, and (-a – bi) mod n = (n – s) + (n – t)i, a question that emerges is whether or not the angles between the complex numbers in these rectangles that were formed when the equivalence classes were graphed, have any patterns? One has to consider these complex numbers as vectors to do these explorations. It was thought some patterns might emerge here, but exhaustive research using spreadsheets did not yield anything specific.
Fourth Research Question
While exploring the rectangles that are formed when a + bi, a – bi, -a + bi, and –a – bi (with integer values for a and b) are considered mod n, another question emerged. What are the sizes and corresponding areas of the rectangles that are formed when the modulus is changed and what is the area of those rectangles? There are some limitations on the size of the rectangles, depending on the modulus, but some patterns do emerge. The following table, Table 2, shows the different rectangles that can be formed and the areas of these rectangles for an odd modulus.
| Modulus | Sizes of Possible Rectangles | Area of Rectangles |
| 3 | 1X1 | 1 |
| 5 | 1X1 | 1 |
| 1X3 | 3 | |
| 3X3 | 9=10-1 | |
| 7 | 1X1 | 1 |
| 1X3 | 3 | |
| 1X5 | 5=6-1 | |
| 3X3 | 9=10-1 | |
| 3X5 | 15 | |
| 5X5 | 25=28-3 | |
| 9 | 1X1 | 1 |
| 1X3 | 3 | |
| 1X5 | 5= 6-1 | |
| 1X7 | 7=10-3 | |
| 3X3 | 9=10-1 | |
| 3X5 | 15 | |
| 3X7 | 21 | |
| 5X5 | 25=28-3 | |
| 5X7 | 35=36-1 | |
| 7X7 | 49=55-6 | |
| 11 | 1X1 | 1 |
| 1X3 | 3 | |
| 1X5 | 5=6-1 | |
| 1X7 | 7=10-3 | |
| 1X9 | 9=10-1 | |
| 3X3 | 9=10-1 | |
| 3X5 | 15 | |
| 3X7 | 21 | |
| 3X9 | 27=28-1 | |
| 5X5 | 25=28-3 | |
| 5X7 | 35=36-1 | |
| 5X9 | 45 | |
| 7X7 | 49=55-6 | |
| 7X9 | 63=66-3 | |
| 9X9 | 81=91-10 |
Table 2: Rectangles that can be formed for an odd modulus.
If we consider the modulus in the first column to be generated by the closed formula 2k + 1 with k as a positive integer greater than or equal to one, then the number of rectangles that can be generated turns out to be the kth triangular number, i.e., the sum of the first “k” positive integers. In other words, in mod 3, where 3 = 2(1) + 1, there is one rectangle that can be formed; in mod 5, where 5 = 2(2) + 1, there are three rectangles that can be formed; in mod 7, where 7 = 2(3) + 1, there are six rectangles that can be formed. So the triangular numbers: 1, 3, 6, 10, etc. , with closed formula, ![]() , where n is a natural number, emerge to represent the number of rectangles that can be formed for larger and larger odd moduli. It should be noted that the indices of the triangular numbers are the numbers being substituted into the closed formula mentioned above. The structure of the table above allows for the triangular numbers to be seen. For example, in mod 9, where the number substituted into the closed formula is four, there are ten different rectangles and ten is the fourth triangular number (index of four). There are 4 rectangles with the first dimension listed as 1, 3 rectangles with the first dimension listed is as 3, 2 rectangles with the first dimension listed as 5, and 1 rectangle with the first dimension listed as 7 and 4 + 3 + 2 + 1 = 10.
, where n is a natural number, emerge to represent the number of rectangles that can be formed for larger and larger odd moduli. It should be noted that the indices of the triangular numbers are the numbers being substituted into the closed formula mentioned above. The structure of the table above allows for the triangular numbers to be seen. For example, in mod 9, where the number substituted into the closed formula is four, there are ten different rectangles and ten is the fourth triangular number (index of four). There are 4 rectangles with the first dimension listed as 1, 3 rectangles with the first dimension listed is as 3, 2 rectangles with the first dimension listed as 5, and 1 rectangle with the first dimension listed as 7 and 4 + 3 + 2 + 1 = 10.
There are some other patterns that appear to emerge, but identifying conjectures for the areas has been more challenging. In the table above, one can see a conjecture that is left for further research: it appears that the areas of the rectangles are either triangular numbers or are differences of non-adjacent triangular numbers.
Before moving on, consideration must be given to the different rectangles that can be formed and the areas of these rectangles for an even modulus. Table 3 below shows this.
| Modulus | Sizes of Possible Rectangles | Area of Rectangles |
| 4 | 2X2 | 4 |
| 6 | 2X2 | 4 |
| 2X4 | 8 | |
| 4X4 | 16 | |
| 8 | 2X2 | 4 |
| 2X4 | 8 | |
| 2X6 | 12 | |
| 4X4 | 16 | |
| 4X6 | 24 | |
| 6X6 | 36 | |
| 10 | 2X2 | 4 |
| 2X4 | 8 | |
| 2X6 | 12 | |
| 2X8 | 16 | |
| 4X4 | 16 | |
| 4X6 | 24 | |
| 4X8 | 32 | |
| 6X6 | 36 | |
| 6X8 | 48 | |
| 8X8 | 64 |
Table 3: Rectangles that can be formed for an even modulus.
Again the triangular numbers appear in the number of different sized rectangles that exist for larger and larger even moduli. However, there is no conjecture that can be made about the areas and that can be left for further research.
Conclusion
This research set out to explore the algebra and geometry of equivalence classes of the complex numbers with integral coefficients mod n, with n as a natural number or positive integer. Algebraically, it was determined that the number of equivalence classes is a perfect square and geometrically the equivalence classes form an ![]() square lattice when graphed on the complex plane. This research also set out to identify patterns that exist in the geometric structures of the equivalence classes with complex numbers mod n. The equivalence classes of all possible positive and negative combinations of a + bi, namely: (a + bi) mod n = s + ti, (a – bi) mod n = s + (n – t)i, (-a + bi) mod n = (n – s) + ti, and (-a – bi) mod n = (n – s) + (n – t)i were explored and it was determined that geometrically a rectangle would be formed in all cases. When the angles between the complex numbers of the equivalence classes above (when the complex numbers were considered as vectors) were explored, nothing was found. Finally, the number of rectangles that can be formed by a different modulus, both even and odd, as the size of the modulus increases, turns out to form a pattern, the triangular numbers.
square lattice when graphed on the complex plane. This research also set out to identify patterns that exist in the geometric structures of the equivalence classes with complex numbers mod n. The equivalence classes of all possible positive and negative combinations of a + bi, namely: (a + bi) mod n = s + ti, (a – bi) mod n = s + (n – t)i, (-a + bi) mod n = (n – s) + ti, and (-a – bi) mod n = (n – s) + (n – t)i were explored and it was determined that geometrically a rectangle would be formed in all cases. When the angles between the complex numbers of the equivalence classes above (when the complex numbers were considered as vectors) were explored, nothing was found. Finally, the number of rectangles that can be formed by a different modulus, both even and odd, as the size of the modulus increases, turns out to form a pattern, the triangular numbers.
Contacts: djohns77@students.towson.edu, jonathan.kraus@howardcc.edu, mlong@howardcc.edu
References
[1] Mardsen, J. E. and Hoffman, M. (1987). Basic Complex Analysis. W.H. Freeman.
[2] Ensley, D. E. and Crawley, J. W. (2006). Discrete Mathematics. John Wiley and Sons, Inc.
[3] Burton, D. M. (1991). Elementary Number Theory. McGaw Hill.