So, You Want to Win Plinko?
Benjamin Marasco, Howard Community College
Naod Assefa, Howard Community College
Mentored by: Dr. Mike Long
Abstract
On January 3rd, 1983 the world was introduced to the Price is Right’s newest game: Plinko (CBS Interactive, n.d.) A contestant stood on the stage at the Plinko board, ready to drop chips in the pachinko-like board, for a chance to win different cash prizes depending on which chamber the chip fell into. Each time the contestant went to drop a chip into the board the roaring voices of the audience would attempt to guide the contestant to where to drop the chip to win the most money. Where should the contestant drop the chip to win the most money? What does the voice of mathematical reason tell the contestant? Most importantly, will the contestant listen to the quiet voice of mathematical reason, or the overpowering voices of the audience? We set out to determine what it was that the quiet voice of mathematical reason was telling the contestant all along. We created computer models to simulate the game and determine where a chip is likely to land depending on where it was dropped. From that, we started asking questions about how much the show’s producers realistically thought they might have to pay the contestant. While building the computer model, we found ourselves asking more questions about what might happen if the board was modified. As it turns out, Plinko type minigames have been popping up in numerous places, with dimensions different from the original game. The computer model was modified to determine how the different dimensions of the board would impact where the chip would land depending on where it was dropped. We revealed what it was that the voice of mathematics should be saying to each contestant to help win the best prize. Now come on down, and take your chances at Plinko, and let your mathematical voice be your guide.
Introduction
Over sixty years ago, the world was introduced to the long-running game show, the Price is Right [1]. In 1972, the game show was revamped into its current form and has been running ever since [1]. On January 3rd of 1983, the contestant who had just bid the closest price on an item won the opportunity to play a new pricing game and that game was Plinko [2]. The game offered the opportunity for a contestant to win up to $25,000 [3]. Although, it was and still is possible that the contestant may not win anything at all. The contestants win monetary values by dropping chips from the top of a large pachinko-like board that has nine possible slots to drop into, thirteen rows of pegs, with every other row offset, and nine chambers at the bottom where the chips can land. The chips fall down the board into the nine chambers across the bottom of the board that are marked with dollar values, including $0. Since these zero value chambers exist, there is a possibility that the contestant does not win anything. The contestants are given one chip and can win up to four other chips by guessing the price of four products.
Some fun facts about Plinko on the Price is Right:
- No contestant has ever landed all five chips in the center chamber, which has the highest dollar value [3]
- To date, the largest amount of money ever won at Plinko is $39,200 [4]
- To maintain consistency, there are only ten Plinko chips, and they are locked up after each use [2]
- The chips were designed to make the “plink” sound on the board [3]
Background Mathematics
The mathematics of the basic Plinko game is pretty straightforward and has been researched. The board itself looks like Figure 1 below.

Figure 1: A standard Plinko board.
As the chips fall through the pachinko-like board, there are two possibilities each time a chip hits a peg. That leads to some interesting mathematics in the number of paths to reach the chambers across the bottom. It might be easier to examine the number of paths on a smaller and simpler Plinko board such as the one in Figure 2 below.
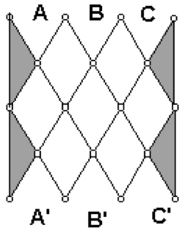
Figure 2: A smaller look at the Plinko board.
The tree diagram that follows, Figure 3 below, shows the probabilities of landing in each of the chambers across the bottom based on the different possible paths through the board. The assumption is also made that the chip is dropped from slot B.
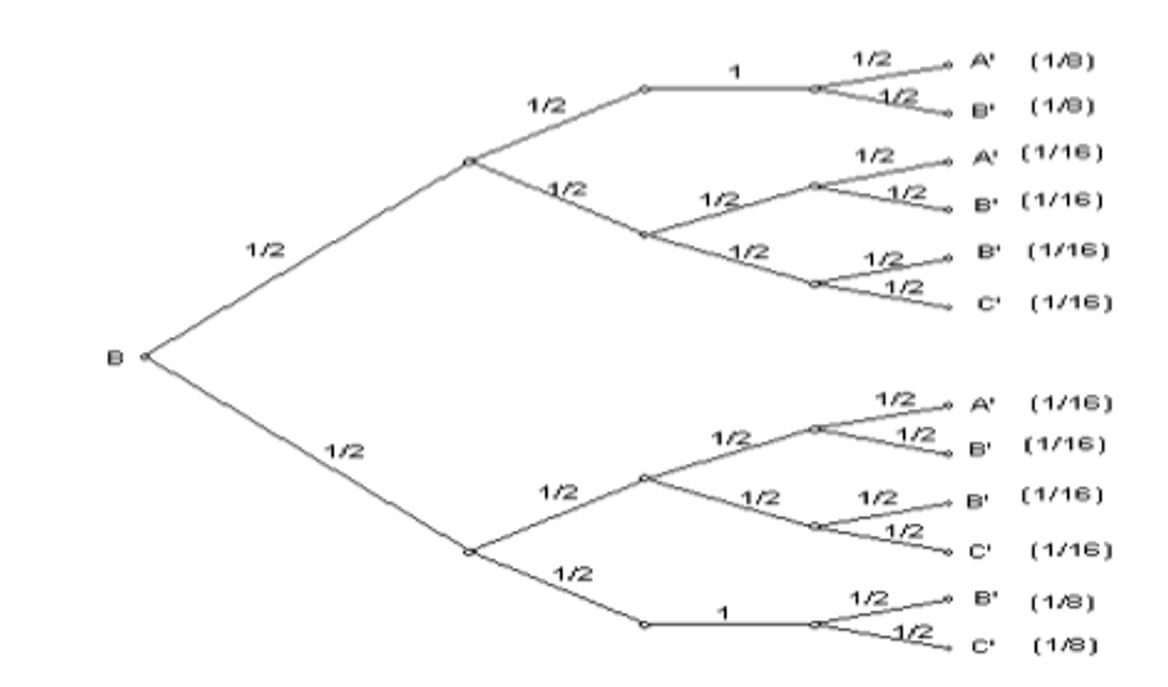
Figure 3: The paths, and probabilities, of chips landing in a certain output slot.
These probabilities make it easier to see the number of paths to the bottom of the actual Plinko board. And it turns out the number of paths involves a simple mathematical structure, Pascal’s Triangle, scene in Figure 4.
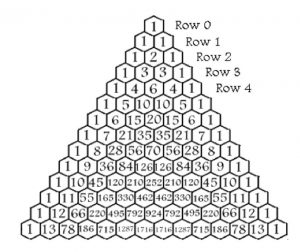
Figure 4: Pascal’s triangle.
The important row here is the line that starts: 1, 12, 66, etc., since that is the 13th row of the triangle. That row would define the number of paths from the middle slot at the top of the board to the bottom of the board except for the fact that the board has only nine chambers across the bottom or is nine columns wide. It is easy to correct for this when it is considered that the chips can bounce off the sides. Table 1 shows the corrections that need to be made given that the board is taller, 13 rows, than it is wide, 9 columns. The 12 that is added to the 66 and the 1 that is added to the 220 account for the chips bouncing off the sides, and we show this mathematically by creating a fold on Pascal’s Triangle after the 66’s in row 13. Think of this as physically folding the left side of the triangle on the rest of the triangle with a fold line on the vertical line between the 12 and the 66. Then note that the 12 lines up with the 66 and the 1 lines up with the 220. The same process can be done on the right side of the triangle where physically the right side of the triangle is folded on rest of the triangle,
| 1 | 12 | 66 | 220 | 495 | 792 | 924 | 792 | 495 | 220 | 66 | 12 | 1 |
| +12 | +1 | +1 | +12 | |||||||||
| 78 | 221 | 495 | 792 | 924 | 792 | 495 | 221 | 78 | ||||
| A’ | B’ | C’ | D’ | E’ | F’ | G’ | H’ | I’ |
Table 1: Corrections for the possible paths on the Plinko board
So there are 78 ways to get into the $100 chambers, (A’ and I’), 221 ways to get into the $500 chambers, (B’ and J’), 495 ways to get into the $1,000 chambers, (C’ and G’), 792 ways to get into the $10 chambers, (D’ and E’), 924 ways to get into the $5,000 or $10,000 chamber, (E’). The difference in the dollar values depends on the year of production. Again, it should be repeated that these are the probabilities when the chips are dropped from the middle slot. Accounting for dropping the chips in different slots across the top simply means moving the fold lines.
Research Question 1
The first research question involves a very interesting concept of mathematics, expected value, and that question is: what do the producers expect to give away on the Price is Right each time that Plinko is played? Even though there are offers of $25,000 or $50,000, depending on whether there is a $5,000 or a $10,000 chamber in the middle of the board respectively, how much do the producers expect to give away? The following table, Table 2, describes the probabilities necessary for the calculation. This table shows the probabilities of falling into each of the nine chambers across the bottom when the chip is dropped from the middle slot at the top.
| P(A’) | P(B’) | P(C’) | P(D’) | P(E’) | P(F’) | P(G’) | P(H’) | P(I’) |
| 0.019 | 0.054 | 0.121 | 0.193 | 0.226 | 0.193 | 0.121 | 0.054 | 0.019 |
Table 2: Plinko probabilities for landing in each chamber
A simple expected value calculation, seen below, can be used to determine the expected value that the producers expect to give away when a chip is dropped from the middle chamber.
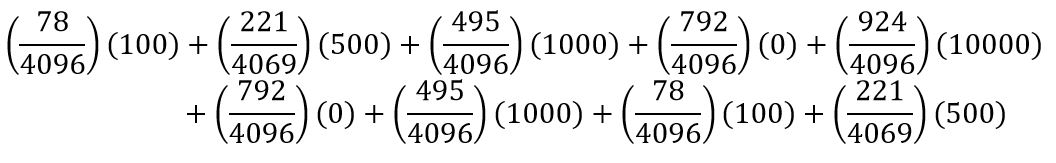
This means the expected value is $2,555.32 per chip for a total of $ 12,766.60 if the player had all five chips. This is the expected value when the middle chamber has a $ 10,000 value and the chips are dropped from the middle slot. This is also when the announcer says there is a chance to win up to $ 50,000. In the real game the contestants are given one chip and have a probability of 0.5 of winning the remaining four chips. That means the actual expected value is $2555.32 +(0.5)($2555.32)+(0.5)($2555.32)+(0.5)($2555.32)+(0.5)($2555.32) = $ 7665.97. Again, all of this only accounts for dropping the chip from the middle chamber. If the contestant moves to one side or the other, the expected value drops and the simulations that are part of this research clearly showed this. This means that the expected value that the producers expect to give away is roughly 15% of what the announcer says the contestants might win.
Research Question 2
The second research question involves the Plinko or pachinko-type boards that have been showing up in various other settings. For example, at some amusement parks, individuals pay for the opportunity to drop a chip down a Plinko or pachinko-type board for the chance to win prizes such as candy, stuffed animals, or passes to the front of the line for a popular ride. The various prizes are listed in the chambers at the bottom, similar to the dollar values on the Price is Right board, with the best prize usually in the middle chamber. The major difference with these boards is the size. These differences in size lead to the research question: what happens to the probabilities or distributions for where the chips land in the chambers across the bottom as the dimensions of the board are changed?
In order to study this question, a Plinko simulator was created. This virtual gameboard was then used to run multiple iterations of the game based on various test parameters. In particular, the virtual gameboard allowed for the height and width of the board to be changed and also allowed for the chip to be dropped from different slots across the top. After each simulation was complete, a graph was displayed that included the distribution of the chips across the bottom of the board, along with the exact numeric values.
The underlying algorithm for the Plinko simulator is based on a two-dimensional array with the width and height of the board being simulated. The values in the array correspond with the slots between a row of pegs, an empty position is represented by a zero, and the current position of the chip is represented by a one. Figures 5 shows this.

Figure 5: A 3×3 Plinko board represented by an array of zeros.
When the chip falls through the board, the probabilities of it moving left or right are determined by a collision system. A collision occurs when the chip falls down and hits one of the pegs on the board. At each peg, the chip has a probability of 0.5 of moving either left or right. This is determined is by a Random Number Generator (RNG) generating a number between 0 and 99, if the number falls between 0 through 49 then the chip moves left, if the number falls between 50 and 99 then the chip falls to the right.
Plinko boards do not typically have a square shape, which is all that can be represented in an array. The rows are staggered and alternate in size to reflect the side walls of the board squeezing in and out (Figure 1). So, the algorithm for the simulation had to use logic to account for the staggered rows. The simulator observes the width of the row that the chip is currently in to determine how the chip can fall to the next row. If the chip’s horizontal position, represented by “n,” was in a row with an odd length then multiple conditions had to be checked:
- If the chip was in the rightmost position, then the chip could only move to the nth column in the next row down
- If the chip was in the leftmost position, then the chip could only move to the n – 1st column in the next row down
- If the chip was in neither of the prior positions, then it could move to either the n – 1st or nth position. It would move to the n – 1st if the output of the RNG was between 50 and 99, or the nth column if the RNG was between 0 and 49.
The rule set for odd length rows allows for the last column to be ignored in rows of even length and thus creating the desired staggered rows as seen in Figure 6 below. The black number one represents the current position of the chip, and, using the odd row-length rules that were defined above, the bold number one represents all possible positions that the chip could move to. The grayed-out position below is the positions that can never be used in order to create the staggered effect of the board.

Figure 6: (Leftmost) An odd row-length simulation, from a chip dropped on the rightmost edge. (Leftmost) An odd row-length simulation dropped from center.
Simulating the even length rows had a similar set of rules, however, the only thing determining which direction the chip moved was the random number generator, RNG. Letting the current position of the chip be represented by n, the chip could move according to following rules:
- If the RNG output was between 0 and 49, the chip would move left to the nth position in the next row;
- If the RNG output was between 50 and 99, the chip would move right to the n + 1st position in the next row.
After the simulator completed one full iteration of the game, it recorded the final position of the chip into the result set and began running the next iteration of the game in the simulation.
Data Collection
For each different size board that was simulated, 1,000 chip drops were run to obtain the distribution data. This simulation was repeated four more times before the size of the board was changed. The first simulation was for a board the size of the Plinko board on the Price is Right: 13 rows by 9 columns. The output from the simulation is in Figure 7 while the distribution can be seen in Table 3 below.
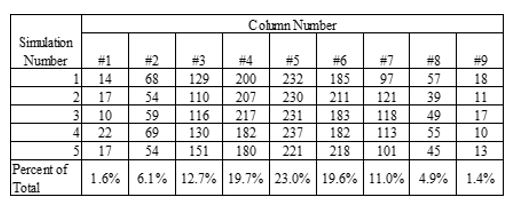
Table 3: Drop distribution for a standard sized Plinko board.
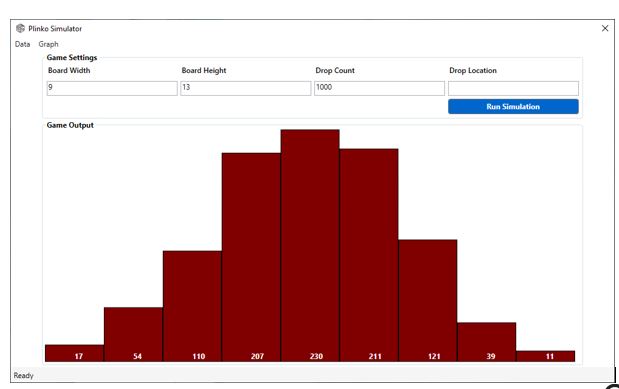
Figure 7: The output of the Plinko simulator, for a 9 column by 13 row standard sized Plinko board.
As the height of the board changes the number of chips falling into each chamber at the bottom, when dropped from the enter chamber, changes. Table 4 shows the results of dropping the chips from the center when the board has different heights.
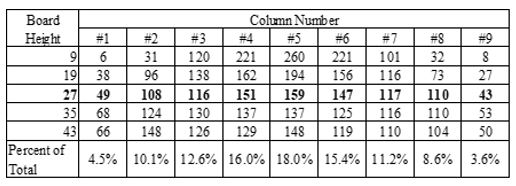
Table 4: The number of chips falling into each camber at the bottom of the Plinko board, when dropped from the center, as the board heights are modified.
As the height of the board is changed, an interesting pattern emerges. The seven inner chambers start to have roughly the same number of chips falling into them. The two outer chambers have roughly the same as well, but they have far fewer chips than the inner chambers. This change in distribution is mostly due to the chips bouncing off the side of the board and appears to occur when the height of the board is three times the width. This was determined through exhaustive simulations. Figures 8 shows the distribution of a 9 column-width Plinko board, with a height of 27, three times the width.
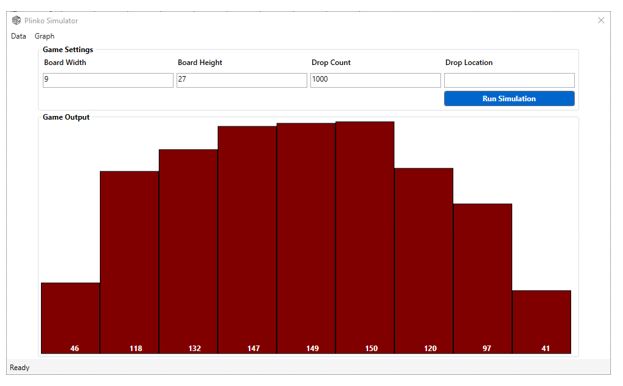
Figure 8: This shows the distribution of a 9 column-width Plinko board, with a height of 27 units.
Conclusion
In this research, there were two major questions that were addressed. After introducing the basic mathematics of Plinko, particularly the number of paths that a chip can take to get from the middle chamber at the top to each of the nine chambers across the bottom, the probabilities for landing in each chamber were determined. The probabilities were then used to compute the expected value or the value the producers of the Price is Right might expect to give away, which was the first research question. This was then compared to what the announcer says a contestant has the possibility of winning. The second research question was to determine how the chips would fall into the chambers across the bottom when the height was modified. An interesting pattern emerged in that a roughly uniform distribution emerges for the chambers that are not on the outside while the outer chambers have roughly the same number of chips, but far fewer than the inner chambers.
Contacts: benjamin.marasco@howardcc.edu, nassefa@howardcc.edu, mlong@howardcc.edu
References
[1] Plinko. (n.d.). Retrieved from The Price Is Right Wiki: https://priceisright.fandom.com/wiki/Plinko
[2] Lewis, D. (2019, December 2). The One Thing You Can’t Take Home from The Price is Right. Retrieved from Now I Know: https://nowiknow.com/the-one-thing-you-cant-take-home-from-the-price-is-right/
[3] CBS Interactive. (n.d.). The Price is Right (Official Site). Retrieved from CBS TV Network: https://www.cbs.com/shows/the_price_is_right/photos/1004546/9-secrets-of-the-price-is-right-s-plinko/3/